Mil-Dot reticle
Some technical and historical information about the Mil-Dot reticle.

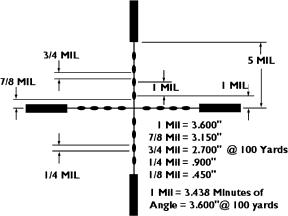This reticle was developed in the late 1970s to help U.S. Marine snipers estimate distances, and is now standard for all military branches. The space between dot centers subtends one milliradian(mil) hence the name mil-dot. Contrary to popular belief it does not stand for "military dot". One mil. subtends 3.6 inches at 100 yards or 36 inches at 1,000 yards. To use this system effectively you must know the size of the target. For instance most people are an average of 6 feet tall or 2 yards. The formula used for determining range to the target is (size of target x 1000 divided by number of mils the target covers). Height of target (yards) X 1,000 = Range (yards) Height of target (mils)

You can do these calculations with a calculator or use a reference table like the ones listed below.
But remember that your answer is only as accurate as the numbers you plug into the formula. An
error of just a 1/4 mil will cause an error in target range. Also an error in estimating the size of your
target will cause an error in target range.

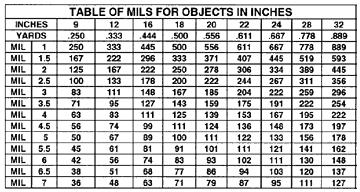
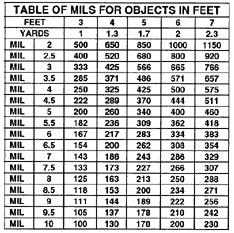
The top line on the table represents the size of the target as measured in feet or inches. The second
line represents the conversion of the foot measurements to yards. The left column shows the mil
measurements to the nearest 1/2mil. The mil scale can be split to the nearest 1/8mil. for a more
accurate range measurement. To use the table follow the instructions below.

Range Estimating with the Mil-Dot Reticle
Dots are spaced in one mil (milliradian) increments on the crosshair. Using the mil formula, a table can be created like the ones above that is based on
the size of the object being targeted. Just look through the scope, bracket the object between dots, and refer to the table for an estimated distance to target.

The radian is a unit less measure which is equivalent, in use, to degrees. It tells you how far around a circle you have gone. 2 PI radians = 360 degrees.
Using 3.14 as the value of PI, 6.28 radians take you all the way around a circle. Using a Cartesian coordinate system, you can use "x"- and "y"-values
to define any point on the plane. Radians are used in a coordinate system called "polar coordinates." A point on the plane is defined, in the polar coordinate
system, using the radian and the radius. The radian defines the amount of rotation and the radius gives the distance from the origin (in a negative or positive
direction).

The radian is another measurement of rotation (the degree/minute/second-system being the first). This is the system used in the mil-dot reticle. We
use the same equation that we used before, but, instead of your calculator being in "degree" mode, switch it to "radian" mode. One milliradian = 1/1000 (.001) radians. So, type .001 into your calculator and hit the "tangent" button. Then multiply this by "distance to the target." Finally, multiply this by 36 to
get inches subtended at the given distance. With the calculator in "radian" mode, type:

tangent(.001)*100*36 = 3.6000012"

So, one milliradian is just over 3.6 inches at 100 yards. If we extrapolate, two milliradians equal about 6 feet at one-thousand yards.

The mil-dot reticle was designed around the measurement unit of the milliradian. The dots, themselves, were designed with this in mind and the spacing
of the dots was also based upon the milliradian. This allows the shooter to calculate the distance to an object of known height or width. Height of the target
in yards divided by the height of the target in milliradians multiplied by 1000 equals the distance to the target in yards. For example, take a 6-foot-tall man
(2 yards). Let's say that the top of his head lines up with one dot and his feet line up four dots down. So: (2/4)*1000 = 500 yards away. This same technique
can be used to estimate lead on a moving target or to compensate for deflection on a windy day.

The distance from the center of one dot to the center of the next dot is 1 milliradian. We are told (by Leupold) that the length of a dot on one of their
reticles is 1/4 milliradian (Given this much information, one can determine that the distance between dots is 3/4 milliradian.).* I use the term "length" because
the mil-dot is not round in all cases. It is oblong in some scopes and round in others (tasco). The width of each dot is an arbitrary distance and is not used
for any practical purpose. Like a duplex reticle, the mil-dot reticle is thicker towards the edges and uses thin lines in the middle where the dots are located
and the crosshairs cross. The distance between the opposite thick portions is 10 milliradians on Leupold scopes.

*NOTE: 1/4 milliradian = .9" and 3/4 MOA = .785", so, obviously, a mil-dot cannot be both 1/4 milliradian and 3/4 MOA. The maker of the mil-dot
reticles for Leupold explains: the dots on their mil-dot reticles are 1/4 mil. They are not 3/4 MOA. Apparently, Leupold just figured that more shooters
understand MOA than milliradians, so they just gave a figure (in MOA) that was close, but not super precise.

To use a mil-dot reticle effectively, all one need remember is that the distance between dot centers is 36" at 1000 yards. This lets you determine the
range of a target of known size. At that point, you can dial the scope in for proper elevation OR use the dots to hold over the proper amount. The
dots on the horizontal crosshair can be used to lead a target (if you know the range to the target, then you'll know the distance between dots, and thus
the distance to lead) or to compensate for deflection.

Minute-Of-Angle
The term "minute-of-angle" (MOA) is used regularly by target shooters at the range, but is probably understood, thoroughly, by few (the same
goes for mil-dots). Defined loosely, one MOA = 1" @ 100 yards; so, if you shot your rifle 5 times into a 100-yard target and every shot went into
a one-inch circle you had drawn on the paper, then your rifle could be said to shoot 1 MOA. Likewise, if every shot goes into a two-inch circle at
200 yards, then you're shooting 1 MOA. A 10-inch group at 500 yards would be 2 MOA.

Now for the fun part. There are 360 degrees in a circle. Each degree can be broken down further into minutes. There are 60 minutes in a degree.
Likewise, there are 60 seconds in a minute. Now, to figure out the distance subtended by 1 minute at any particular distance, we need merely to plug
those two values into a simple trigonometric equation. The tangent function fits the bill nicely. Here's the equation:
tan(angle) = distance subtended/distance to the target (units must be consistent--e.g., 1/36 of a yard [1"] divided by 100 yards)
Now, we know the angle (1 minute or 1/60 of a degree) and we know the distance to the target (100 yards), but we need to figure out the actual distance
subtended at the target (i.e., is 1 MOA actually 1" @ 100 yards?). What we need to do is solve for "distance subtended." Here's our final equation:

tan(angle)*distance to the target = distance subtended

Make sure your calculator is in "degree" mode (as opposed to "radian" or "gradian") and type in 1/60 (for degrees) and hit the "tangent" button. Then
multiply that by 100 yards. This should give you the distance (in yards) subtended at 100 yards. Multiply this by 36 to get inches. The answer should be:

1.047197580733"

This is just a hair over the commonly quoted "one inch." At 1000 yards, this would be almost 10 1/2 inches. Apparently, it is just a coincidence
that 1 MOA happens to be REALLY close to 1" @ 100 yards. It is, however, quite convenient.

Back